Question Find all the critical points of the nonlinear system dx dt = x y x 2 xy dy dt = x 2 y and identify their types The sketch a possible phaseportrait for the system Solution To find the critical points we need to find all solutions to the simulatanous equations x y x2 xy = 0 x2 y = 0 In general there is no guaranteed method for doing this, so be creative!List of nonlinear ordinary differential equations Jump to navigation Jump to search See also List of nonlinear partial differential equations A–F Name Order Equation Applications Abel's differential equation of the first kind 1 = Mathematics Abel's differential equation of the second kind Algebraically, linear functions are polynomials with highest exponent equal to 1 or of the form y = c where c is constant Nonlinear functions are all other functions An example of a

Linear Non Linear Functions Edmodo
Y=x^2+13 linear or nonlinear
Y=x^2+13 linear or nonlinear- Equation is linear if dependent variable y is not being multiplied by variable x sin (y) and cos (y) make equation non linear Now i went to a site and they said following equation is linear x^2y'' xy' (x^2v^2)y = 0 The equation of a nonlinear function has at least one exponent higher than 1, and the graph of a nonlinear function is a curved line Linear functions can be




Linear Or Nonlinear Functions From A Table Youtube
Examples include x=3 or y=2 which are linear in one variable, y=2x3 or 2x3y=6 which are linear in two variables, xy3z=10 which is linear in three variables etc The graphs of linear The difference between the linear and nonlinear functions are their degrees For linear functions, the highest order is only 1 while more than for those nonlinear functions If these are presented in graphs, linear functions would generate straight lines while parabola or other curved lines will be generated for nonlinear functions State the degree of each of the following and identify it as a linear or nonlinear relation a y = x2 State the degree of each of the following and identify it as a linear or nonlinear relation a y = x2 2x 1 b 3x 3y = 6 Categories English Leave a Reply Cancel reply
The solving of the nonlinear circuits is complex than the linear circuit and there is a lot of data, information is required to solve the nonlinear circuits Due to a lot of change in the technology, we can simulate and analyze the output curves of linear and nonlinear circuits with the help of the circuit simulation tools like MultisimNote To see if a table of values represents a linear function, check to see if there's a constant rate of change If there is, you're looking at a linear function! To Solve Your System of Integer Nonlinear/Linear Equations, You Essentially Just Replace the Two Equations Immediately Below with Your Equations Jsun Yui Wong To illustrate, the computer program listed below uses the following integer nonlinear equations from Anonymous 9 xy = 48 x/y y/x = 7875 where x and y are positive integers
Q Determine if the point (1, 2) is a solution to the following system 4x 2 5y 2 2x 63y 108 = 0 x 2y = 3 answer choices Yes, because it works in one equation Yes, because it works in the both equations No, because it works in neither equation No, because it works in only one equationDetermine if a relationship is linear or nonlinear Determine if a relationship is linear or nonlinear If you're seeing this message, it means we're having trouble loading external resources on our website If you're behind a web filter, please make sure that the domains *kastaticorg and *kasandboxorg are unblocked 14Linear & Nonlinear Linear & Nonlinear Linear systems, converting nonlinear systems to linear ones, and differential equations 32 min read Linearity and linear systems are important in science and engineering for two reasons Linear systems are easy to think about – at least when compared to nonlinear systems!



Linear Equation Wikipedia
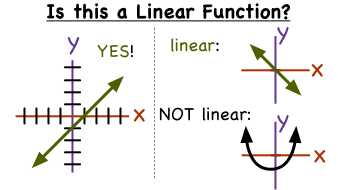



How Can You Tell If A Function Is Linear Or Nonlinear From A Graph Virtual Nerd
We will be using these same methods as we look at nonlinear systems of equations with two equations and two variables A system of nonlinear equations is a system where at least one of the equations is not linear For example each of the following systems is a system of nonlinear equations { x 2 y 2 = 9 x 2 − y = 9 { 9 x 2 y 2 = 9 y = 3Signal and System Solved Questions on Linear and NonLinear SystemsTopics Discussed1 Linear and nonlinear systems2 Effect of timescaling on the linearNonlinear Estimation Many models have no convenient linear representation Sometimes we know or believe our data have a particular nonlinear structure Want to exploit this for better estimation and inference Simple example instead of linear regression model We may believe in nonlinear regression model Here, is nonlinear function of some




Answer Choices Y X 10 Linear Y X 10 Non Linear Y 10x 1 Linear Y 10x 1 Nonlinear Brainly Com




Linear Or Nonlinear Functions From A Table Youtube
Y = X 4 Linear Nonlinear Answers 2 Get Other questions on the subject Mathematics Mathematics, 1800, sophiamoser Julius sold five times as many computers as sam sold last year in total, they sold 78 computers how many computers did julius sell? The difference between nonlinear and linear is the "non" OK, that sounds like a joke, but, honestly, that's the easiest way to understand the difference First, I'll define what linear regression is, and then everything else must be nonlinear regression I'll include examples of both linear and nonlinear regression modelsIt is linear because y (t) is linear function of x () Irrespective of x may be function of linear or nonlinear function of t (it doesn't matter sint or t^2 or 2*t)so it is linear



1




Linear And Nonlinear Functions Identifying Functions On Tables
Remember that this has its roots in linear algebra y = m x b You can analyse functions termbyterm to determine if they are linear, if that helps The first time a term is nonlinear, then the entire equation is nonlinear Remember that the x s can pretty much do or appear however they want, since they're independent As nonlinear dynamical equations are difficult to solve, nonlinear systems are commonly approximated by linear equations (linearization) This works well up to some accuracy and some range for the input values, but some interesting phenomena such as solitons , chaos , 9 and singularities are hidden by linearizationWas asked on View the answer now
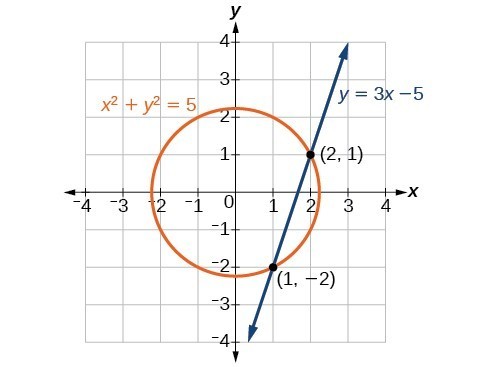



Methods For Solving A System Of Nonlinear Equations College Algebra



Linear And Nonlinear Functions Identifying Functions On Tables
are these linear or nonlinear?30 Questions Show answers Question 1 SURVEY 300 seconds Q Is this function linear or nonlinear? \ y(x_0) = y_0 \ then we can uniquely solve for \(C\) to get a solution This immediately shows that there exists a solution to all first order linear differential equations This also establishes uniqueness since the derivation shows that all solutions must be of the form above



Linearization Linear Approximation Of A Nonlinear Function X Engineer Org




Differential Equation 2nd Order 5 Of 54 Linear Vs Non Linear 2nd Order Diff Eqn Youtube
Simple way to find if something is linear or non linear is by looking at the powers If it's anything over power of 1 it isn't linear x (3x10) = 3x (squared) 10x Which makes it nonlinearC is the yintercept For example y = 2x 1, here the equation has the highest degree as one So it is a linear equation A nonlinear equation will not match this equation You can also test an equation is linear or nonlinear by plotting it on the graphIs y (t)=x (sin t) linear or nonlinear?




The Graph Of Approximate Nonlinear Function Y F X By A Linear Download Scientific Diagram




B Consider The System Of Nonlinear Equations G Z Chegg Com
Does the following table represent a linear equation so let's see what's going on here when X is negative 7 y is 4 then when X is negative 3 y is 3 so let's see what happened toward what our change in X was so our change in X and I could even write it over here our change in X so going from negative 7 to negative 3 we had an increase in 4 and X and what was our change in Y and1 Newton's linear model for F(X) Newton's method for solving a nonlinear equation f(x) = 0 can be generalized to the ndimensional case The value of the variable and the value of the function are now ndimensional vectors, and when we can, we will write these as Xand F(X) to remind us that they are no longer scalars Since our examplesThis tutorial shows you how to tell if a table of values represents a linear function




Ccs 8 F A 3 Proving Y Mx B Is Linear And Y X 2 Is Nonlinear By Murphy S
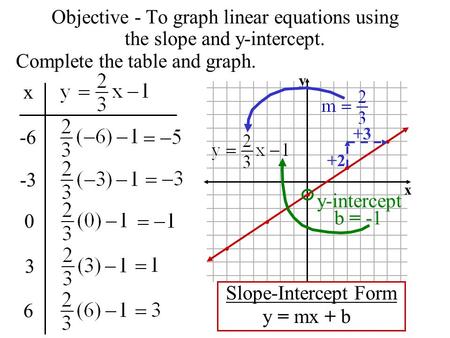



Linear And Nonlinear Functions Identifying Functions On Tables Graphs And Equations Ppt Download
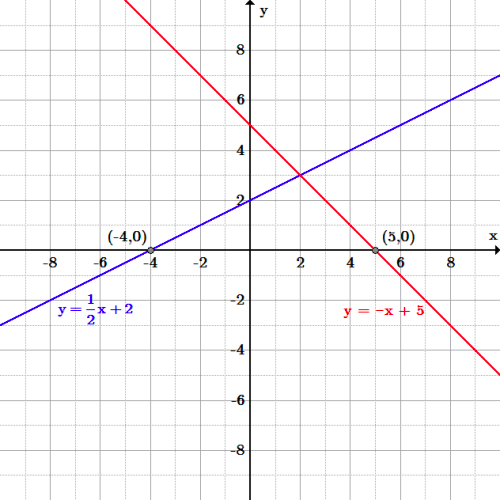
A nonlinear equation is such which does not form a straight line It looks like a curve in a graph and has a variable slope value It looks like a curve in a graph and has a variable slope value The major difference between linear and nonlinear equations is given here for the students to understand it in a more natural wayTherefore, the solution set to the given system of nonlinear equations consists of two points which are (– 3, 4) and (2, –1) Graphically, we can think of the solution to the system as the points of intersections between the linear function \color{red}x y = 1 and quadratic function \color{blue}y = {xNonlinearsystemofequationscalculator x^2y=5, x^2y^2=7 en Related Symbolab blog posts High School Math Solutions – Systems of Equations Calculator, Nonlinear In a previous post, we learned about how to solve a system of linear equations In this post, we will learn how




Linear And Non Linear Systems Solved Problems Part 1 Youtube




Linear And Nonlinear Functions Identifying Functions On Tables Graphs And Equations Irma Crespo Ppt Download
(ii)Perform a linear stability analysis of each equilibrium (iii)Carefully sketch the phase plane Problems 7 and 8 feature nonhyperbolic equilibria 7Consider the nonlinear system x_ = y;A linear equation will have constantly increasing y values and a straight line, while a nonlinear equation will have outputs increasing at a nonconstant rate and a curved graph After awhile, determining these functions will become easy and you will be able to tell which function you have simply by looking at the equation itselfLINEAR REGRESSION 6 Graph of Y=X2u u is lognormally distributed with a mean of 1 b
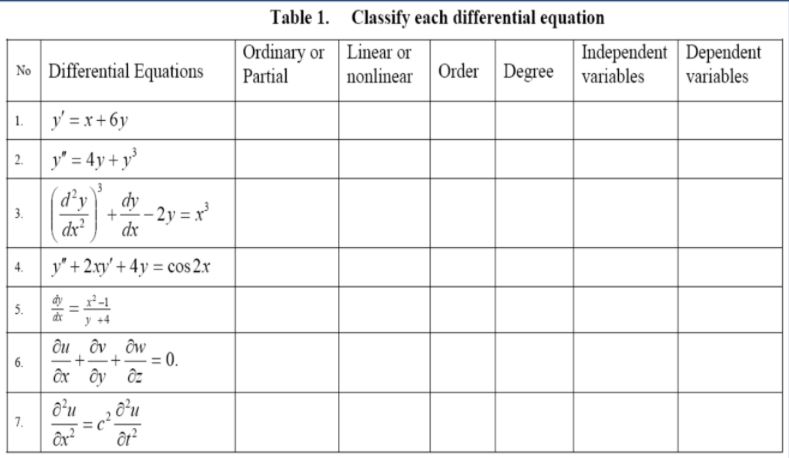



Answered Table 1 Classify Each Differential Bartleby




Ml Basics Regression How To Tell If A Dataset Is Linear Or Not By Abhinav Mahapatra Medium
If variable y is 1st degree but the variable x has a degree other than 0 or 1, it will be a nonlinear function of x Examples y = x^2 25 (x is not first degree) y = 5x 2 x^3 (x is 3rdA non linear Diophantine equation is every Diophantine equation which is not linear For instance, the equation x 2 3 y 3 = 35 is a nonlinear Diophantine equation There is no universal method for solving nonlinear Diophantine equations, however, there are a number of "methods" that can help us in solving some special types of nonTranscribed image text 2) Solve the following system of nonlinear equations by using the fi (x, y) = x(x 1) 2y 18 = 0 fixed – point iteration method Start with Xo = and yo = 11 and carry out the first three iterations Firstly, write the general formula of this 12(x, y) = (x 1)2 ( – 6)2 – 25 = 0 method for solving system of nonlinear equations and analyse the convergence




Plsssssssssss Help Click To Show Whether Each Equation Represents A Linear Or Nonlinear Brainly Com




What Makes A Differential Equation Linear Or Non Linear Mathematics Stack Exchange
Answer choices Linear Nonlinear The given equation is not linear because the power of x is not 1 but 1 Given y=4/x The given equation is not linear because the power of x is not 1 but 1 Let us rewrite the equation as y=4x^(1) Look at this graph of the given equationY = x (3x 10) is this linear or non linear?




Linear And Nonlinear Function Distinction Ck 12 Foundation




Nonlinear Function Definition Examples Video Lesson Transcript Study Com
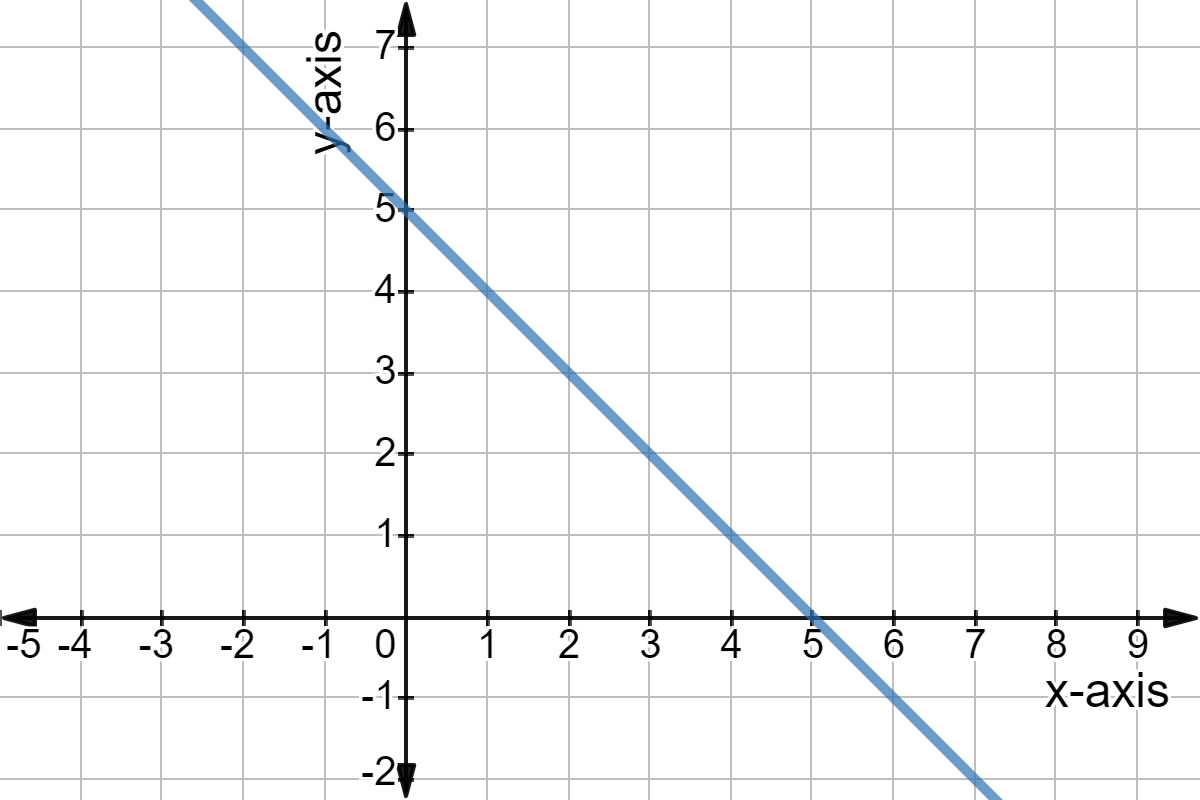
A linear function has an equation that can be written in the form of y=mxb Equations whose graphs are not straight lines are called nonlinear functions Determine whether the function is linear or nonlinear The graph of a linear function is a straight line This graph is not a straight line So, this is a nonlinear functionY_ = x y3 (i)Sketch the nullclines and find the equilibria (ii)Perform a linear y=x5 is a linear equation that has been shifted down 5, the slope is still 1 So if you plug in points for x, you can find the position easily When x=0, y=5




Linear And Nonlinear Functions Identifying Functions On Tables Graphs And Equations Ppt Download




Solved Able Or Equation Represents A Linear Or Nonlinear Chegg Com
Answers 1 continue Mathematics, 2106Free linear equation calculator solve linear equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Given we have xy the equation is not linear 2) y 2(x 9) = 0 y 2x 18 = 0 y = 2x 18 This is linear 3) 3y 6(2 x) = 5 3y 12 6x = 5 3y = 5 12 6x 3y = 6x 7 y = 2x 7/3 This is linear 4) 2(y x) = 0 2y 2x = 0 2y = 2x y = x So this means that this is linear




Linear And Nonlinear Functions Identifying Functions On Tables Graphs And Equations Ppt Download



Biomath Linear Functions
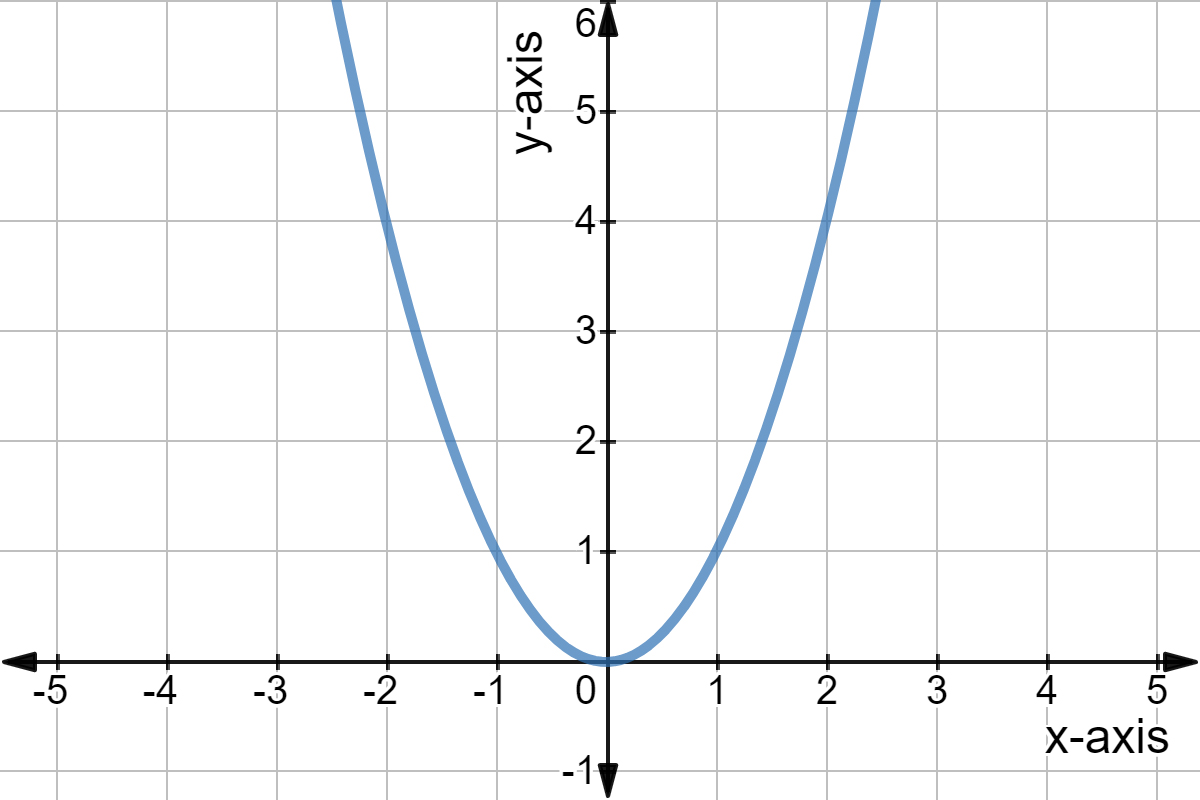
Y = x2 y = x 2 A linear equation is an equation of a straight line, which means that the degree of a linear equation must be 0 0 or 1 1 for each of its variables In this case, the degree of variable y y is 1 1 and the degree of variable x x is 2 2




Linear Non Linear Functions Edmodo




Nonlinear Function Definition Examples Video Lesson Transcript Study Com



Nonlinear Functions




Graph Using Intercepts



Systems Of Non Linear Equations Chilimath




8 F A 3 Powerpoint Lesson Lesson Teaching




Logistic Regression As A Nonlinear Classifier By Ashok Chilakapati Towards Data Science




Y X Linear Vs Non Linear Ppt Download




Is Y T X Sin T Linear Or Non Linear Quora



How Is The Signal Y T X T X T 1 Nonlinear Quora




Determine If Each Function Is Linear Or Nonlinear Brainly Com




Linear And Nonlinear Functions Ppt Video Online Download
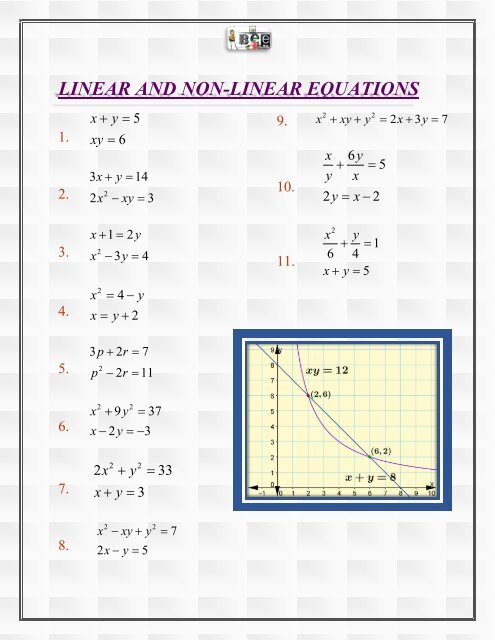



Linear And Non Linear Equations




Linear And Nonlinear Functions Identifying Functions On Tables
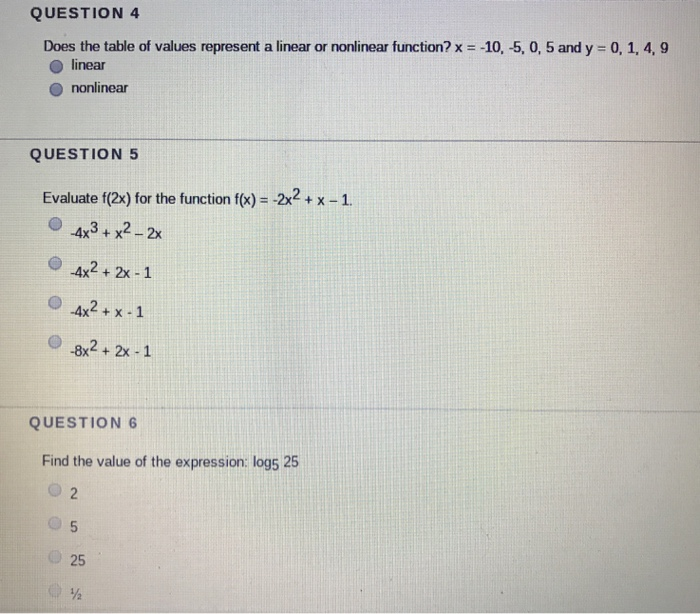



Question 4 Does The Table Of Values Represent A Chegg Com




Click To Show Whether Each Equation Represents A Linear Or Nonlinear Function Linear Brainly Com




Non Linear Regression By Linearization Write A Chegg Com




Linear And Nonlinear Functions Ppt Download




Linear And Nonlinear Function Distinction Ck 12 Foundation




1 State Whether The Given Ordinary Differential Chegg Com




1 The Differential Equation 2 X Y 2x 3 Y 0 Chegg Com
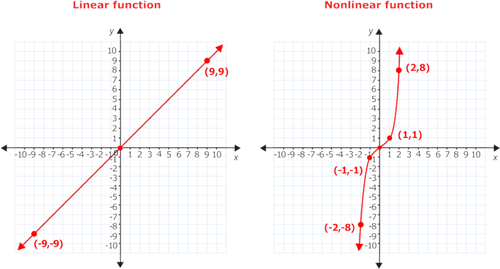



Linear And Nonlinear Function Distinction Ck 12 Foundation




Linear Nonlinear Functions Table Video Khan Academy




Nonlinear Function Definition Examples Video Lesson Transcript Study Com




Recognizing Linear Functions Video Khan Academy




Identifying Linear Nonlinear Functions Using Graphs Tables Video Lesson Transcript Study Com




8 6 4 Comparing Linear And Nonlinear Functions Ppt Download




Nonlinear Function Definition Examples Video Lesson Transcript Study Com




Ccs 8 F A 3 Proving Y Mx B Is Linear And Y X 2 Is Nonlinear By Murphy S
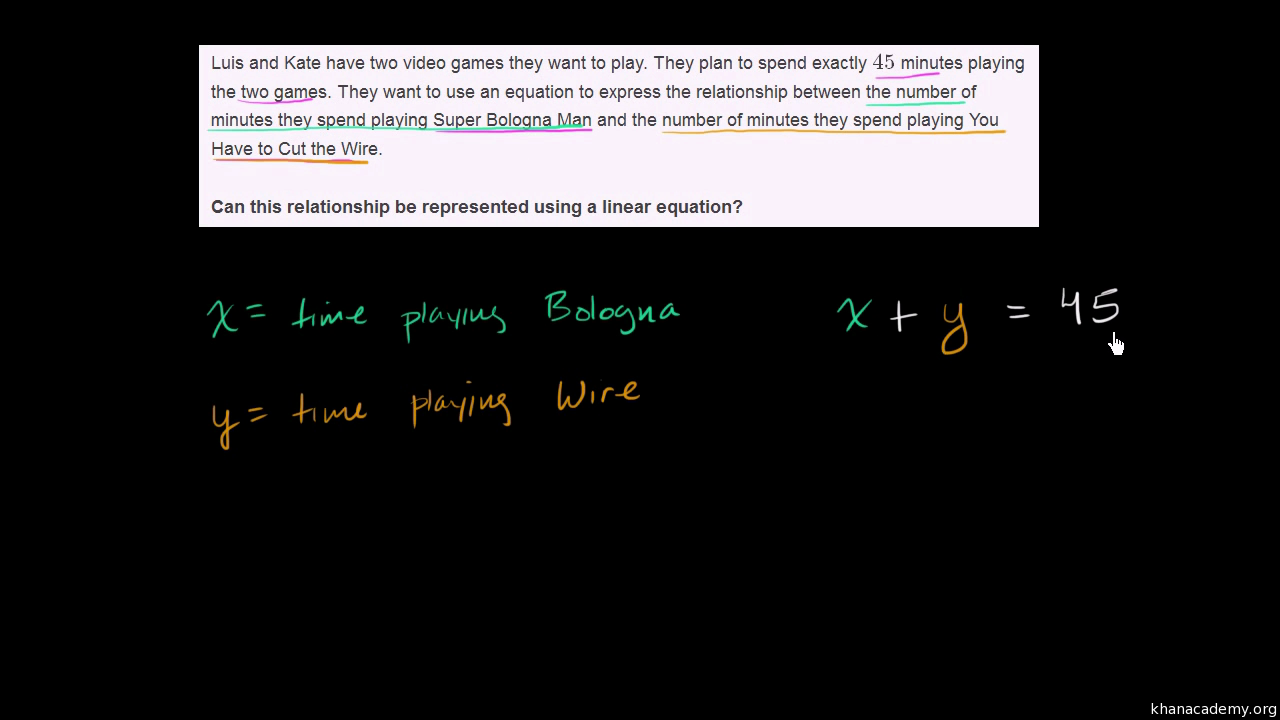



Linear Nonlinear Functions Word Problem Video Khan Academy




Constant Multiples Of Solutions A Show That Y Chegg Com




Identify Linear Quadratic And Exponential Functions N Distinguish Quadratic And Exponential Functions As Nonlinear Using A Graph And Or A Table Ppt Download




Linear And Nonlinear Functions Ppt Download




A I Know That The Nonlinear Parts Are Y T Dy T Dt Chegg Com
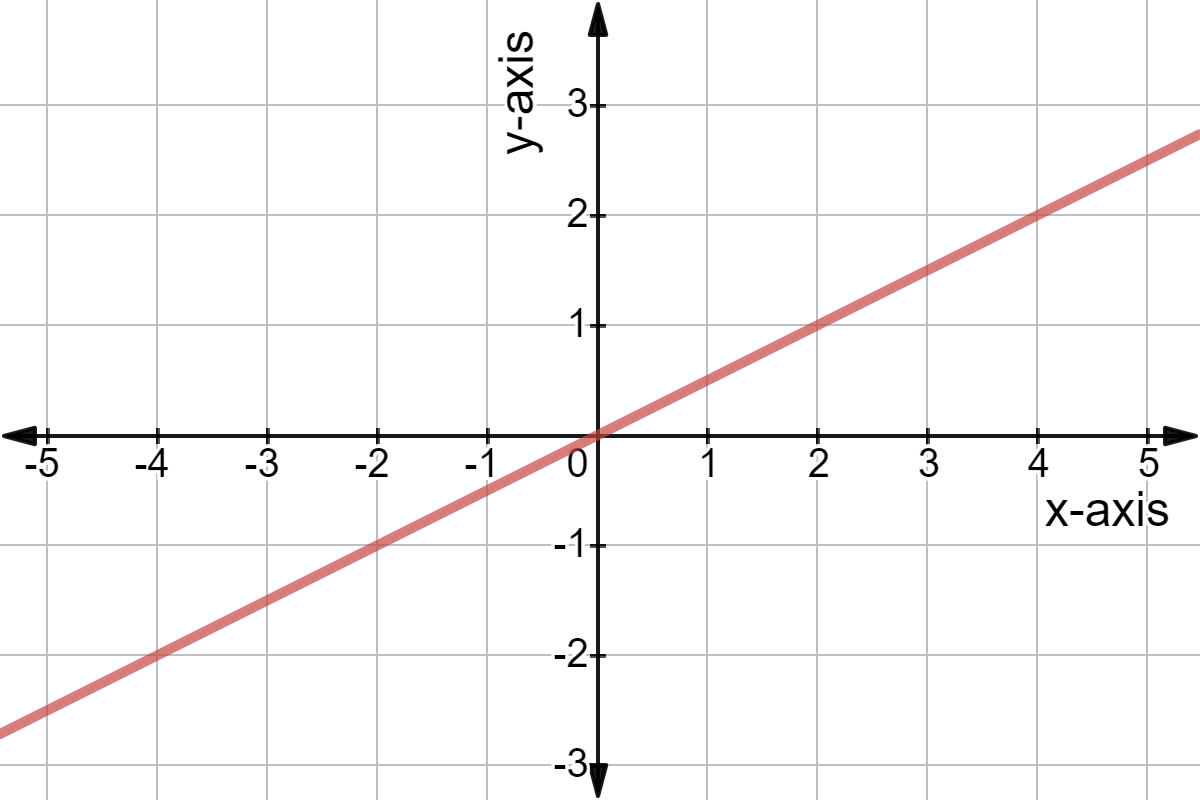



Intro To Linear Vs Nonlinear Functions Expii
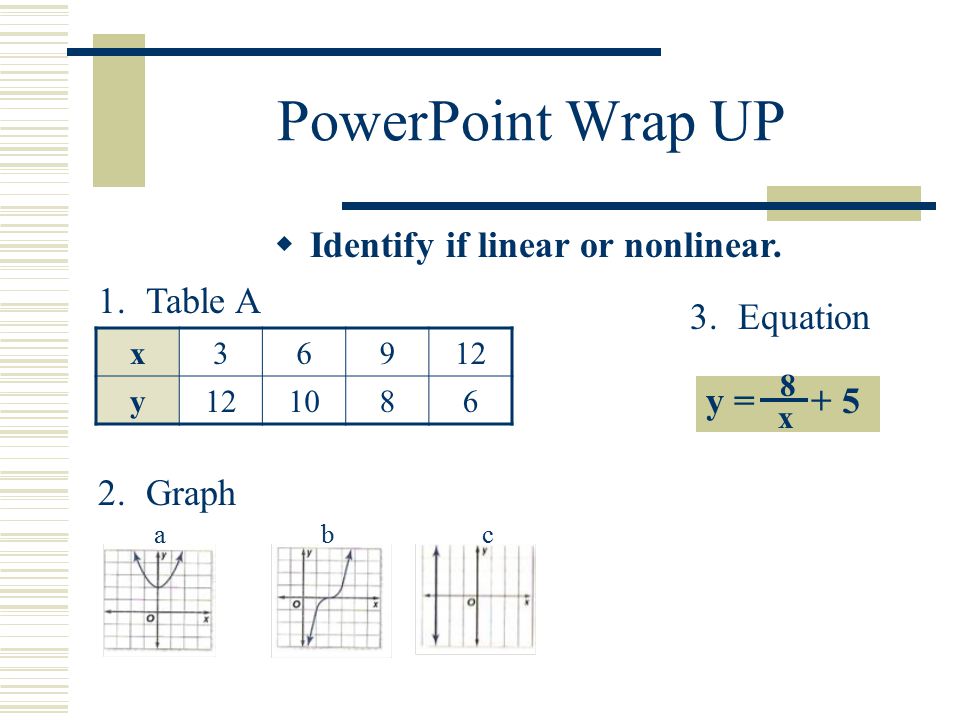



Linear And Nonlinear Functions Identifying Functions On Tables Graphs And Equations April 27 Ppt Download




Linear Functions Length Of A Side Of A Square Yard Compare And Contrast Yards To Feet Number Of Feet Number Of Yards Yards To Square Yards Length Ppt Download




Linear And Nonlinear Relationships Learning Target I Can




Linear And Nonlinear Functions Ppt Download



Intro To Linear Vs Nonlinear Functions Expii




Determine If Each Function Is Linear Or Nonlinear Linear Nonlinear 3x Y 12 Brainly Com




How To Convert Non Linear Equations To Linear Form Y Mx C Youtube



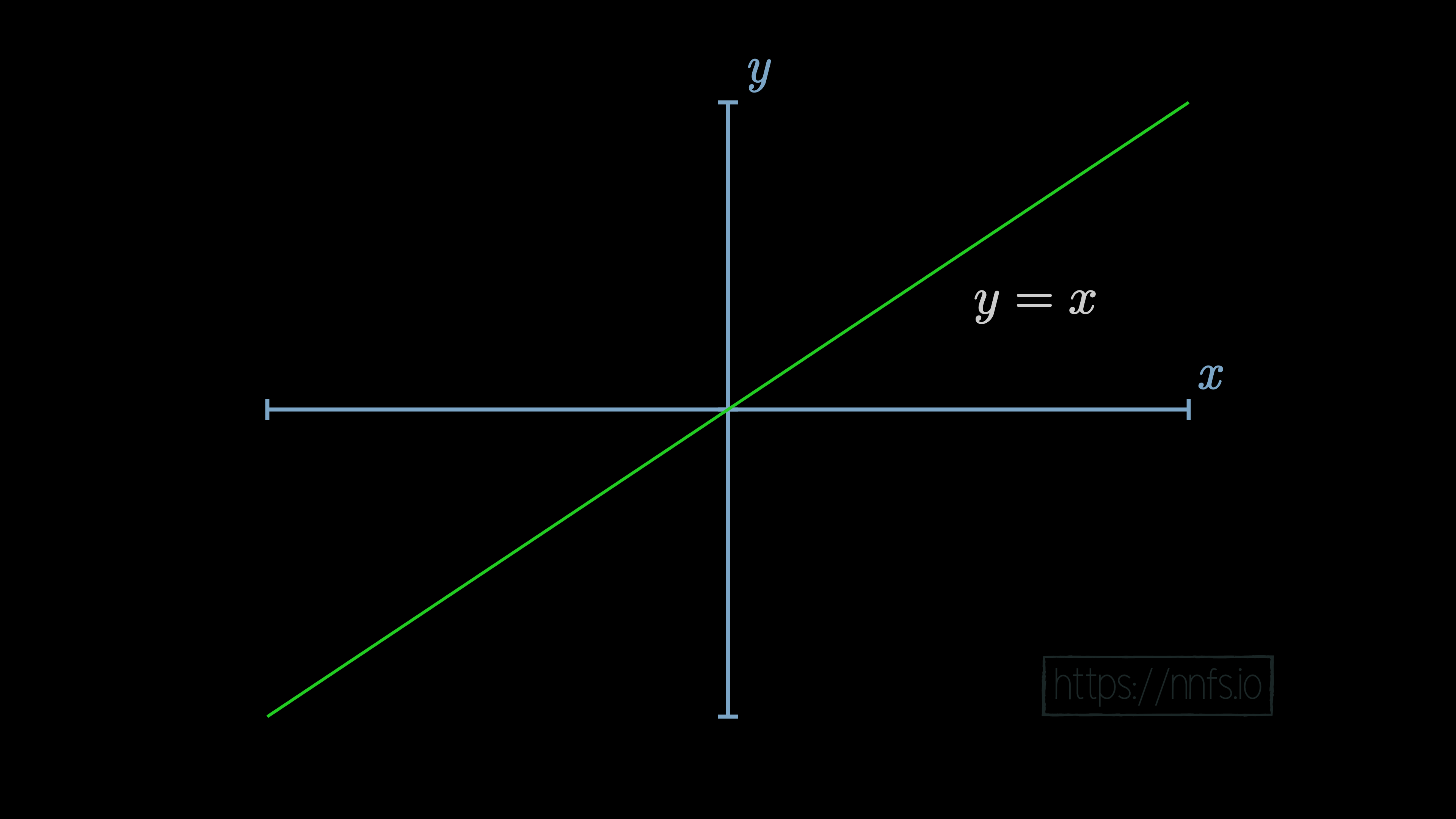
Introduction To Linear Functions Boundless Algebra



Linearization Linear Approximation Of A Nonlinear Function X Engineer Org




Does The Table Above Represent A Linear Or Nonlinear Function Explain A Nonlinear Function B Brainly Com




Linear Nonlinear Functions Table Video Khan Academy




4 3 Patterns And Non Linear Functions Ppt Video Online Download




Recognizing Linear Functions Video Khan Academy




Please Helpis The Function Linear Or Nonlinear Y 1 X A Linear B Nonlinear Brainly Com



1



Intro To Linear Vs Nonlinear Functions Expii



Why How Two Or More Hidden Layers W Nonlinear Activation Functions Works With Neural Networks Deep Learning




How To Define Linear And Non Linear Differential Equation Mathematics Stack Exchange




Classify The Following Equations As Linear Nonlinear Chegg Com




Finding X And Y Intercepts Of The Graph Of A Non Linear Equation Youtube



1




Graphing Linear And Nonlinear Equations With Tables Of Values Worksheet Equations Values Worksheet Graphing
/LinearRelationshipDefinition2-a62b18ef1633418da1127aa7608b87a2.png)



Linear Relationship Definition




Identifying Linear Nonlinear Functions Using Graphs Tables Video Lesson Transcript Study Com
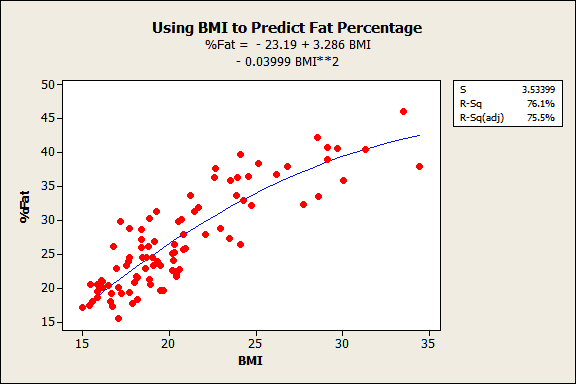



What Is The Difference Between Linear And Nonlinear Equations In Regression Analysis




Linear Vs Nonlinear Functions Criterion A 1 2 Chegg Com
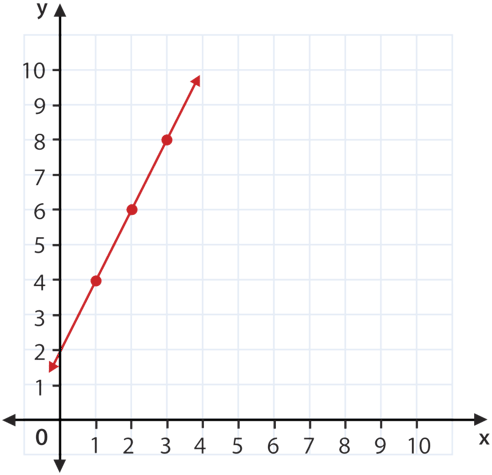



Linear And Nonlinear Function Distinction Ck 12 Foundation




Ccs 8 F A 3 Proving Y Mx B Is Linear And Y X 2 Is Nonlinear By Murphy S




Solving Non Linear Systems By Graphing Youtube




Linear And Nonlinear Functions Ppt Download
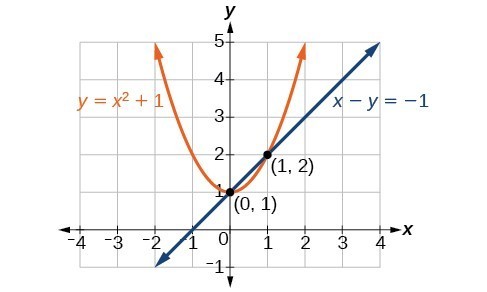



Methods For Solving A System Of Nonlinear Equations College Algebra




Linear And Nonlinear Function Distinction Read Algebra Ck 12 Foundation




Classify Each Of The Differential Equations As Linear Chegg Com



Linear Nonlinear Functions Teacher Guide




Consider The Non Linear System Of Differential Chegg Com




Question Tell Whether Each Function Is Linear Or Non Linear Choices A Function A Is Non Linear Brainly Com




Ch 1 2




Solved In Problems 87 95 Determine If Each Equation Is L Chegg Com




Rules For Functions Linear Or Nonlinear Focus 6
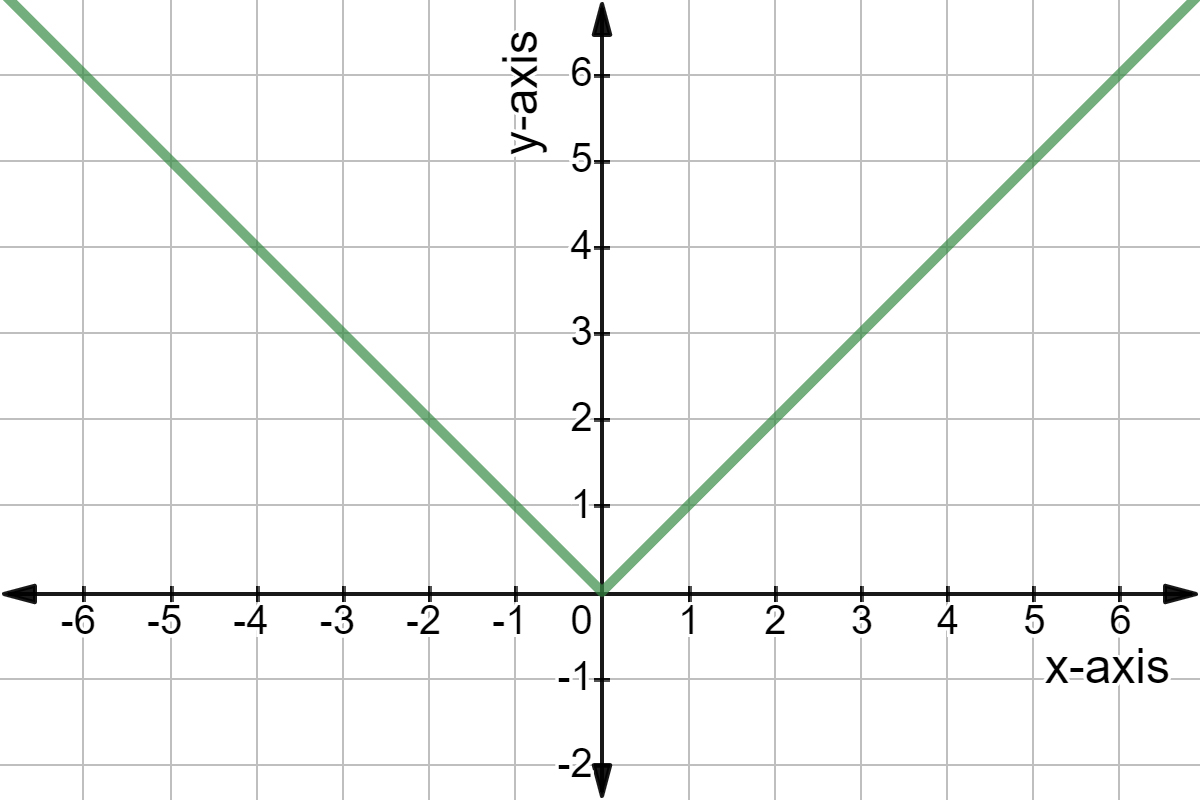



Intro To Linear Vs Nonlinear Functions Expii
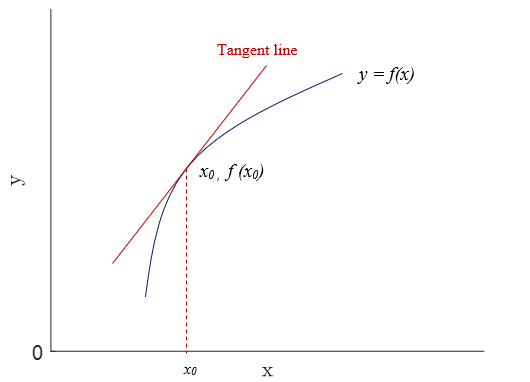



1 Slope




Graphing Linear And Nonlinear Equations With Tables Of Values Worksheet Equations Values Worksheet Worksheets



1



0 件のコメント:
コメントを投稿